Extended Abstract: Download PDF
Introduction
Blackjack is a popular casino game that is played all over the world, and many have come up with strategies to try to beat the dealer, such as card counting. Such exploits have been highlighted in popular culture through the movie 21, which was based off of the book Bringing Down the House, by Ben Mezrich. The game itself is highly based on probability and seems simple, but effective strategies for beating the dealer are not readily apparent without thorough probabilistic analysis. Because of this, many inexperienced players will make moves based on intuition or gut feeling without taking into account the probabilities behind their decisions. As such, the game is a good choice for applying machine learning algorithms to see whether a computer can devise an effective strategy for playing given enough trial games, so that it can beat the dealer a significant percentage of the time.

Figure 1: Example of a simulated game of blackjack
Our task is to create a machine that can learn to play the card game Blackjack strategically based upon information learned from previous games it has played through using reinforcement learning techniques. In order to do so, it is necessary to build a Blackjack game implementation that gives feedback and rewards to the machine, which learns the rules of Blackjack as well as advanced gameplay strategies in the process. Our task demonstrates the viability of teaching machines to play deeply intuitive, probability-based games such as Blackjack. It also shows how machine learning techniques in general can have real-world impact, since Blackjack is one of the most popular casino games in the world and generates significant revenue for casinos worldwide.
Design
Before we could implement any machine learning techniques to train a computer to play blackjack, we needed to create an interface that would allow us to simulate a game of blackjack. This involved writing card, deck, player, and dealer classes in Python, allowing a computerized dealer to deal cards to a simulated player that would be taught the game of blackjack through reinforcement learning techniques. We chose to implement a simplified version of the game, with one dealer and one player, no bets or monetary sums, and no splitting. This allowed us to focus purely on the playing strategy involved in the game, since splitting is essentially like creating another player, while the monetary sums involved are important only in a competitive context.
In regards to the details of gameplay, the deck of 52 cards is shuffled before each round, and Aces are valued as 11's automatically, unless it would cause the total value of the hand to go over 21, in which case Aces are revalued as 1's as necessary. The player goes before the dealer, either hitting or standing at each point in its turn according to its learned strategy, then the dealer goes. We programmed the dealer to hit until reaching 17 or more, then standing, which is a rule for dealers that is frequently used in many casinos.
After researching reinforcement learning techniques, we settled on using Q-learning to teach our simulated player how to play blackjack, because it learns the state-action value function and the exploration policy at the same time, while also being an off-policy method. To select which action to choose at each decision point, we chose to use an epsilon-greedy policy that selected the action with the highest Q-value, except for epsilon percentage of the time, when it selected an action randomly. Because we used Q-learning, our data set consisted of a table of Q-values stored in a CSV (Comma Separated Value) formatted file, which would be continuously updated after each hand according to the formula:
Q(s, a) ← (1-alpha)Q(s, a) + alpha(r + gamma * maxa’Q(s’,a’))
We initially tried implementing a version of Q-learning that had 2 Q-values, one for hitting and one for standing, but found that this caused the player to develop a far too aggressive strategy, making it hit all the time and never standing. We then implemented a version that had 36 Q-values, with a Q-value for hitting and standing at every possible hand state in the game. After this, we added Q-values to differentiate between whether or not the player had an Ace in its hand, meaning every value hand had 4 Q-values, one for (no Ace, stand), one for (no Ace, hit), one for (has Ace, stand), and one for (has Ace, hit). This brought our total number of unique Q-values up to 72, one for every significant state in the game.
There have been implementations of Q-learning with regards to the game of blackjack done before, such as at: http://ape.iict.ch/teaching/AIGS/AIGS_Labo/Labo5-RL/rlbj.html; however, our game design was coded independently and goes beyond what has been done before by taking into consideration the presence of Aces when calculating Q-values, as well as fine-tuning the rewards system, which we detail below. Our implementation is therefore more complex and nuanced, acknowledging the strategic depth inherent in the game of blackjack.
Results and Analysis
To judge the performance of our algorithm, we made our interface play a large number of games and recorded the win percentage of our simulated player over the dealer, comparing the win percentage of the learned strategy with that of a random playing strategy and the dealer’s strategy. Our results before optimizing rewards and formula parameters showed that our player was clearly learning the rules of the game and refining its strategy after every round of play, since its win percentage went up rapidly within the first few hundred games it played, as shown in Figure 2. We then tweaked alpha (learning rate) and gamma (discount factor), but found that they had no significant effect on win percentage, which consistently converged to approximately 36% after around 5,000 games, coming within 4% of the win percentage of the dealer’s strategy.
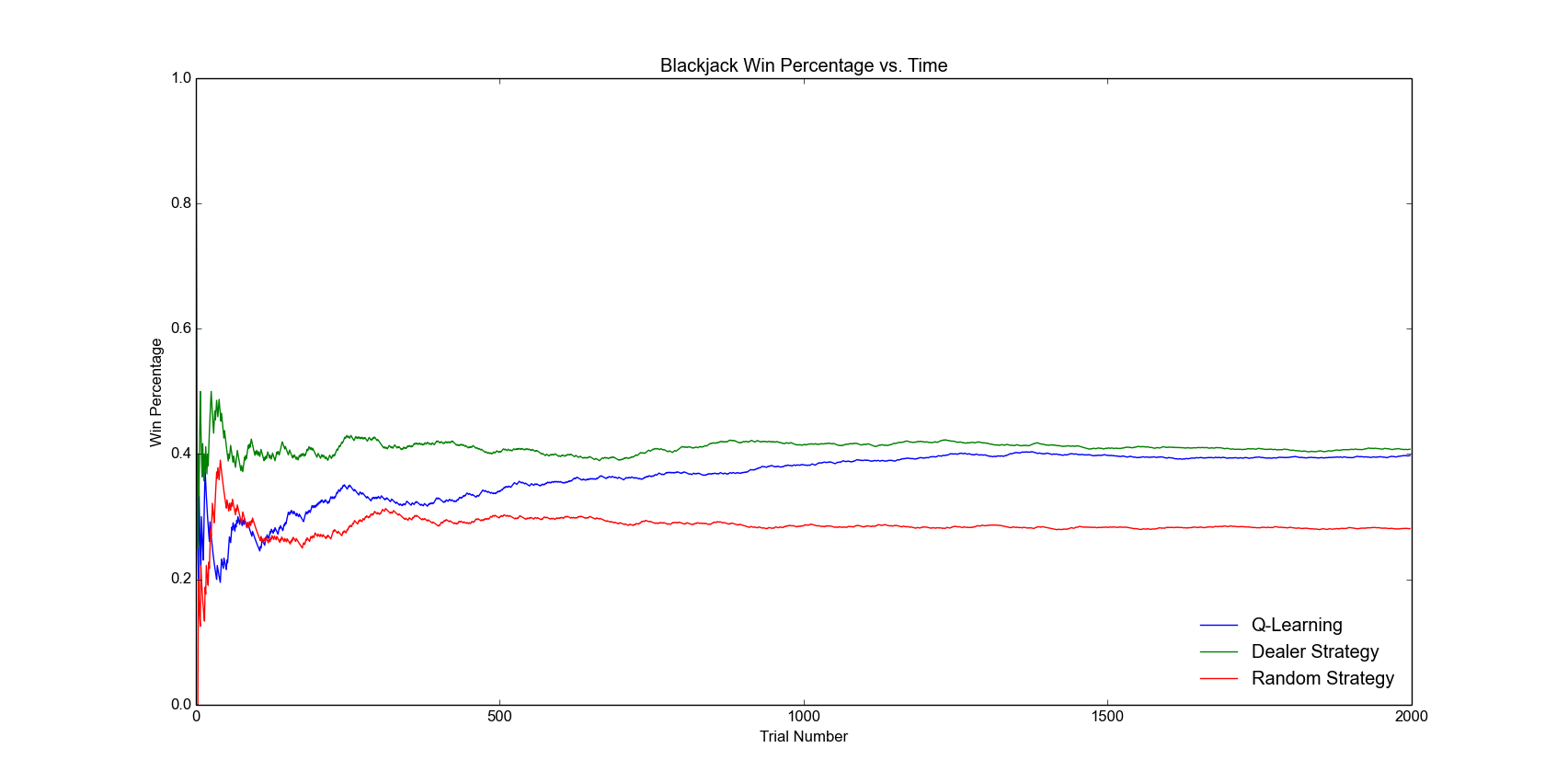
Figure 2: Win percentage increases rapidly in the first few hundred games
After that, we tweaked the rewards given to the simulated player. For choosing to hit, the player receives a reward value equal to the value of the player’s hand plus a random integer between 1 and 5. If the player has a ‘Flipped’ ace, an ace with a value of 1, then this reward is negated, and if the value of the reward is greater than 22, the player receives a 0 instead. For choosing to Stand, the player receives a value of -1 if the decision leads to a loss. Otherwise, the player receives a value equal to the reciprocal of 22 minus the value of the player’s hand. These tweaked reward values led to a significant increase in win percentage, such that win percentage stabilized at 39.5% after 100,000 games, coming within 0.3% of the dealer’s strategy’s win percentage of 39.8%. These results are shown in Figure 3.
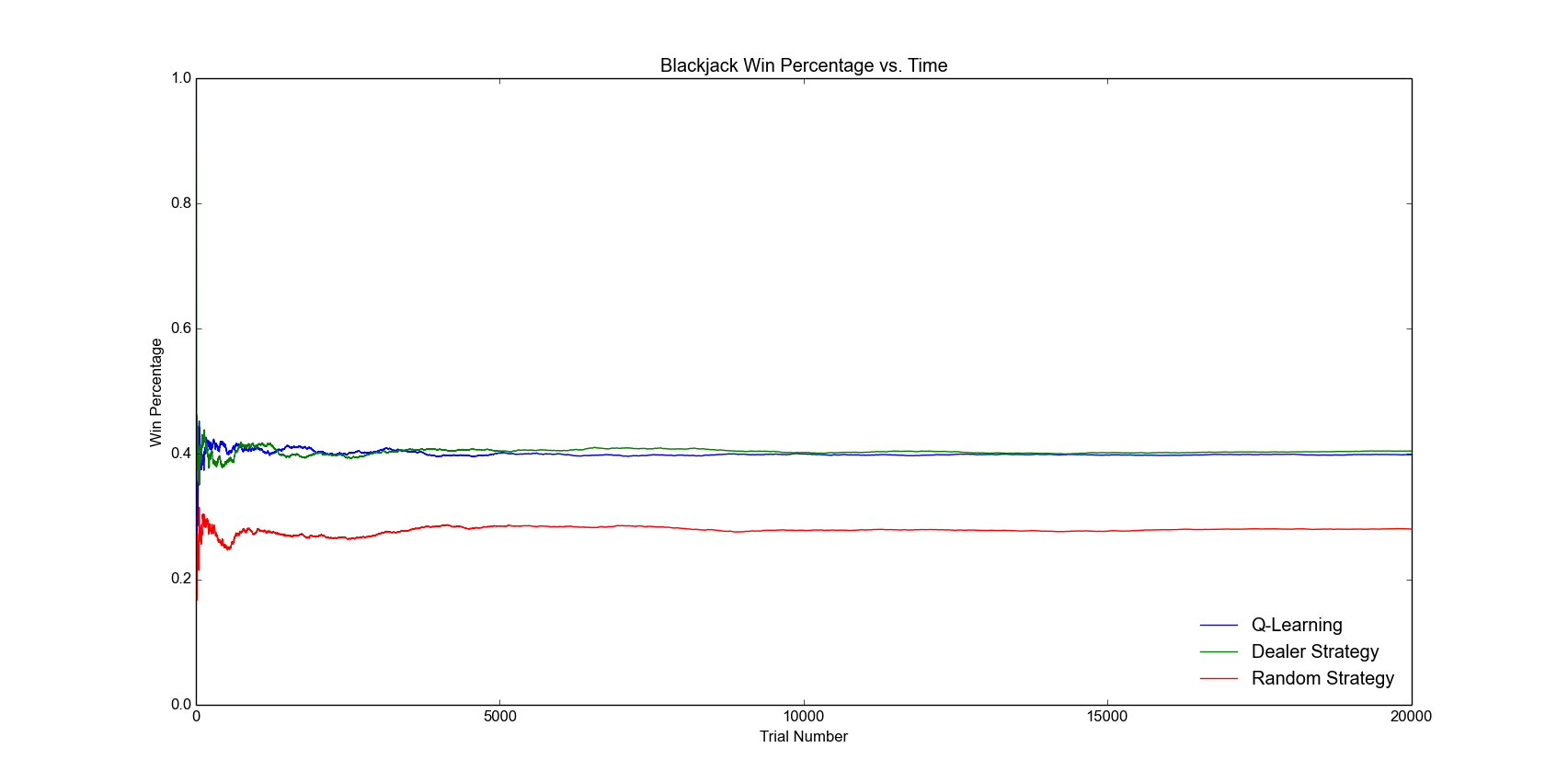
Figure 3: Win percentage of learned strategy converges to that of Dealer’s strategy
Conclusion
By implementing a version of the Q-learning algorithm in Python, we were able to build a machine blackjack player that quickly learns the basic rules of the game and eventually learns more advanced strategies, allowing it to achieve a much higher win percentage than if it were randomly choosing actions. Over the course of many games, the win percentage of the learned strategy converges to that of the Dealer’s strategy. In future implementations of our simulated playing environment, we intend to add the ability to split hands, as well as adding in a monetary system that allows the player to double down and allows us to measure the player’s performance through the total amount of money it accumulates over the course of many games. Ideally, this would allow the learned strategy to surpass the Dealer’s in terms of performance. However, in its current state, Hackjack demonstrates the viability of machine learning techniques, such as Q-Learning, for providing usable solutions to problems involving a significant degree of uncertainty.
Contact the Authors
Joonyong Rhee
JoonyongRhee2016@u.northwestern.edu
Alexander Wenzel
AlexanderWenzel2017@u.northwestern.edu
Taylor Zheng
TaylorZheng2015@u.northwestern.edu